Содержание кривых участков пути

Кривые участки пути составляют на сети дорог около 30 % раз­вёрнутой длины главных путей. В кривых путь работает более на­пряжённо, чем в прямых. Связано это с тем, что в кривых по срав­нению с прямыми участками пути значительно выше уровень го­ризонтальных поперечных сил, которые тем больше, чем меньше радиус кривой и чем выше скорости движения поездов.

Дорожный мастер и бригадир пути должны изучать состояние кривых участков пути на своём околотке, выявлять интенсивность возникновения здесь неисправностей, их характер и причины.

При визуальных осмотрах кривых выявляют целостность эле­ментов верхнего строения пути, земляного полотна, сооружений, об­ращая внимание прежде всего на провисание рельсов, резкие про­садки, отбои рельсовых нитей, резкие “углы” и извилины в плане, на слитые зазоры в стыках и т.д. Кроме того, оценивают равномер­ность загрузки обоих рельсов, т.к. от этого во многом зависит ус­тойчивая работа всех элементов пути на данном участке.

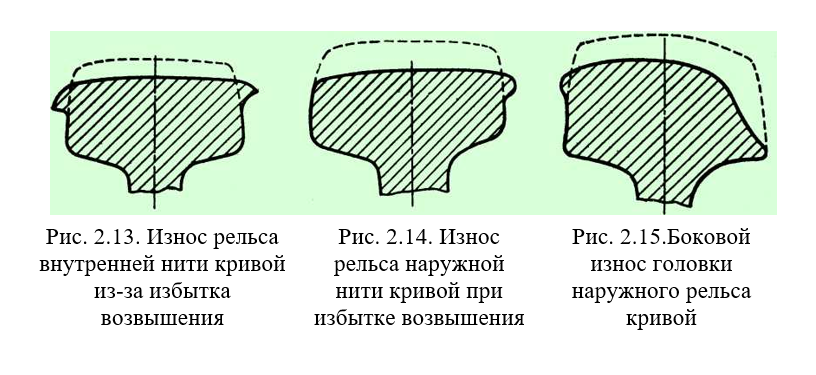
Интенсивное смятие головки внутреннего рельса кривой (рис. 2.13) при отсутствии или значительном боковом износе го­ловки наружного рельса или даже образование на ней наплыва металла (рис. 2.14) является признаком чрезмерного возвыше­ния наружного рельса. В этом случае следует повторно провести расчёт возвышения наружного рельса, основываясь на фактически реализуемых скоростях движения, которые определяются по ско­ростемерным лентам локомотивов.

При интенсивном боковом износе головки наружно­го рельса кривой (рис. 2.15) следует проверить работу рельсосма- зывателей и правильность их установки.

Визуальный осмотр пути сочетается с измерениями ширины ко­леи, выявлением отступлений по уровню в пределах круговой кри­вой, плавности и величины отвода возвышения наружного рельса в переходных кривых, а также совпадения его начала и конца с на­чалом и концом переходной кривой.

Устойчивость колеи в кривых определяется состоянием промежуточных скреплений, плотностью прилегания подошвы рельса к плоскости подкладок, состоянием шпал.

В кривых не следует допускать кустовой негодности шпал.

На звеньевом пути отступления в плане возникают прежде все­го в зоне стыков и интенсивно развиваются при наличии отрясения шпал.

Несвоевременное выполнение работ по рихтовке кри­вой приводит к неравномерному износу рельсов, а также к появле­нию отступлений по ширине колеи.

В значительной степени стабильное положение рельсошпальной решетки в кривых зависит от состояния балластной призмы и обес­печения отвода воды от неё. Плотное опирание шпал на балласт является непременным условием обеспечения стабильности пути в

плане и профиле. Отрясение шпал возникает, как правило, в пер­вую очередь в стыках, в том числе и сварных. Если своевременно не выполнить работы по подбивке пути, число отрясенных шпал будет расти, и в этих местах образуются потайные толчки, просад­ки, углы в плане, а при загрязнённом балласте — выплески.

В кривых, особенно при радиусах менее 1000 м, более часто при­ходится выполнять выправку пути в плане, профиле и по уровню, исправлять ширину колеи и замену шпал на деревянных шпалах, а на железобетонных шпалах — замену нашпальных и подрельсо­вых прокладок.

Одинаковые неисправности пути в переходной кривой более опасны, чем в круговой. В первую очередь это относится к перекосам, просадкам и коротким неровностям в плане, а также к сочетаниям этих неисправностей. Наличие их может вызвать раз­грузку рессорного комплекта тележки с вползанием гребня колеса на наружный рельс кривой и последующим сходом подвижного со­става. Особенно неблагоприятно эти неисправности сказываются на выходных переходных кривых, где колесо движется по наруж­ной нитке под уклон в пределах отвода возвышения.

Сплошную выправку кривых наряду с устранением боль­шего числа отступлений в плане, профиле и по уровню назначают для ликвидации несовпадений начала и конца переходных кривых по кривизне и возвышению, а также для приведения возвышения на­ружного рельса круговой кривой в соответствие с расчётным. При выправке кривой в профиле вначале поднимают внутреннюю нить, а наружную ставят по уровню с учётом расчётного возвышения.

Рихтовку кривой осуществляют на всём её протяжении, захватив примыкающие прямые участки. В ряде случаев, когда на­блюдается расстройство отдельных участков кривой, производят их частичную рихтовку. При всех вариантах выправку кривых в плане необходимо вести на основании расчётных сдвигов, полу­ченных по данным съёмки, выполненной накануне работ. Рихтов­ка кривых “на глаз”, как правило, не даёт положительных резуль­татов, т.к. при этом не удаётся добиться одинаковой кривизны в круговых кривых и плавного её изменения в переходных.

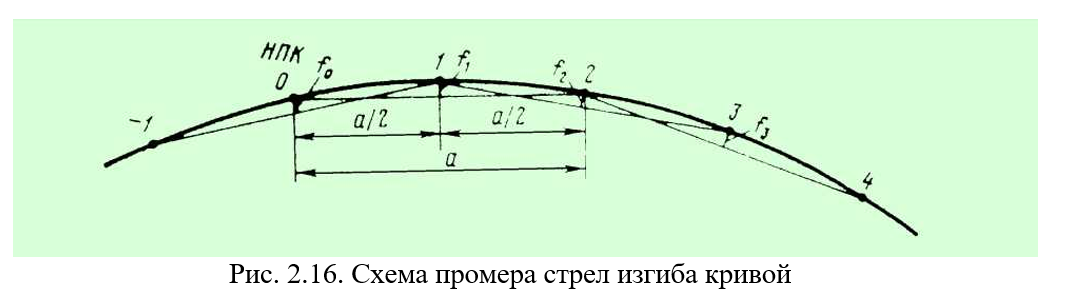
Проверка правильности положения кривой в плане обычно проводится измерением стрел изгиба кривой ƒ от се­редины хорды а, соединяющей две точки кривой (рис. 2.16).

 

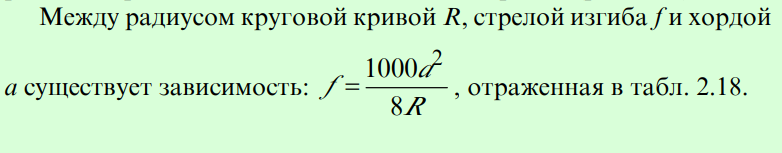
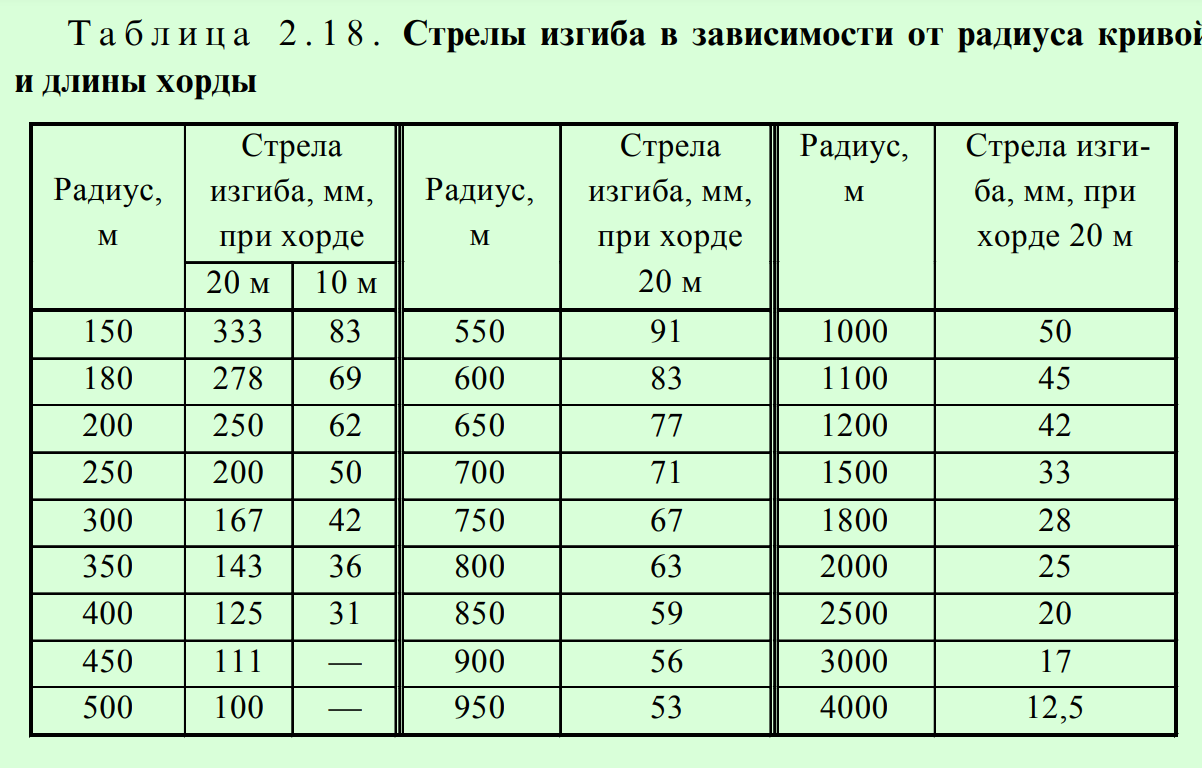
В пределах переходной кривой ПК стрела изгиба увеличивает­ся равномерно от нуля до величины стрелы круговой кривой. Стре­лы изгиба в пределах переходной кривой, за исключением начала ПК и конца, определяют по формуле

Съёмка кривых проводится два раза в год: весной и осе­нью. При осенней проверке кривых одновременно со съёмкой стрел изгиба измеряют возвышения наружного рельса, а в кривых, име­ющих уширение колеи, также и ширину колеи. Кроме того, съёмку кривых выполняют за два-три дня до намечаемой рихтовки, т.к. под воздействием поездов кривая может несколько изменить своё положение, что приведёт к потере точности выправки.

Съёмка кривых выполняется бригадой из трёх человек: техник и два монтёра пути.

Разбивку и съёмку кривых ведут по наружной рельсовой нити, которую называют рихтовочной. Примыкающие к кривой прямые часто имеют искривления, поэтому начальная точка промеров вы­бирается на прямом участке пути на расстоянии 20—30 м от види­мого начала кривой. Аналогично определяется и конечная точка про­меров. Кривая и примыкающие к ней прямые размечают на равные участки длиной 10 м (при радиусах кривой 400 м и менее — длиной 5 м). Разметку и нумерацию точек ведут в направлении нарастания километров. Точки деления предварительно намечают меловыми вертикальными рисками на внутренней грани головки и шейки рельса, а затем закрепляют их на шейке рельса белой масляной крас­кой. Это обеспечивает промер и рихтовку кривых всегда в одних и тех же точках и исключает повторные работы по разбивке кривых.

В качестве измерительной хорды используется шнур из капро­новой нити толщиной 0,6—0,8 мм. Его прижимают к незакруг­лённой части рабочей грани головки наружного рельса в точках, смежных с той, где измеряется стрела. Перед измерением шнур натягивают так, чтобы не было провисания, а колебания шнура останавливают.

Стрела изгиба измеряется линейкой с обрезанным “под нуль” концом. Измерения ведут против средней точки деления между ра­бочей гранью рельса и шнуром с точностью до 1 мм.

Если у входа в кривую или выхода из неё образовался обрат­ный изгиб, то стрелы этого изгиба записывают со знаком минус. Концы шнура в этом случае прижимают к нерабочей грани рельса за пределами наплыва.

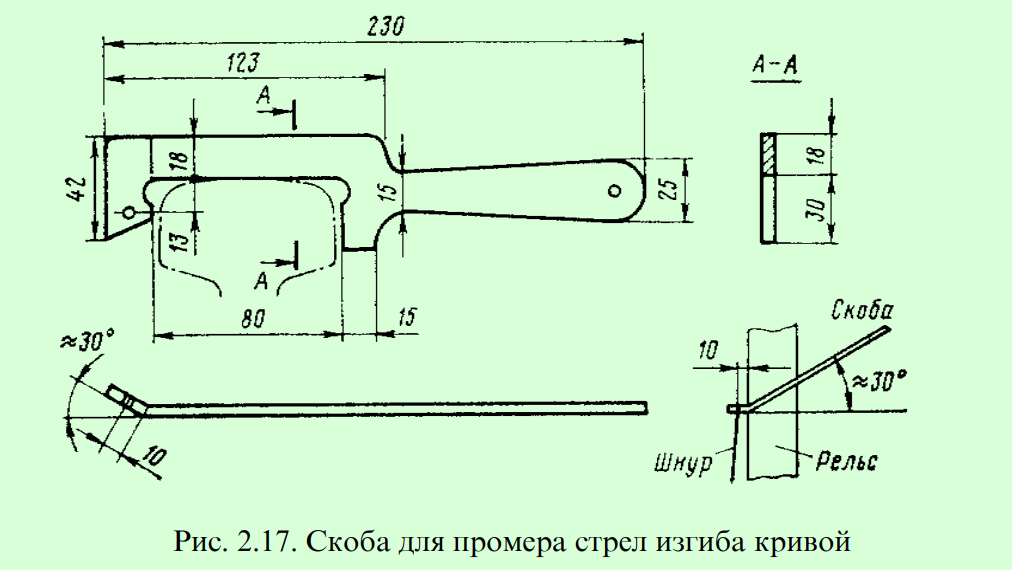
Для облегчения съёмки кривой можно использовать надёжное и простое приспособление конструкции ЦНИИ в виде скобы для промера стрел изгиба кривой. Комплект состоит из измеритель­ной линейки и двух одинаковых скоб (рис. 2.17) со шнуром.

Кроме стрел изгиба в процессе съемки кривой измеряют также расстояние от оси пути до бровки земляного полотна и до всех близ­ко стоящих сооружений, устройств. На двухпутных участках опре­деляют расстояние между осями путей. По этим данным выявляют точки, не подлежащие сдвигу, в зависимости от ширины обочин, земляного полотна, наличия искусственных сооружений, переездов и других местных условий.

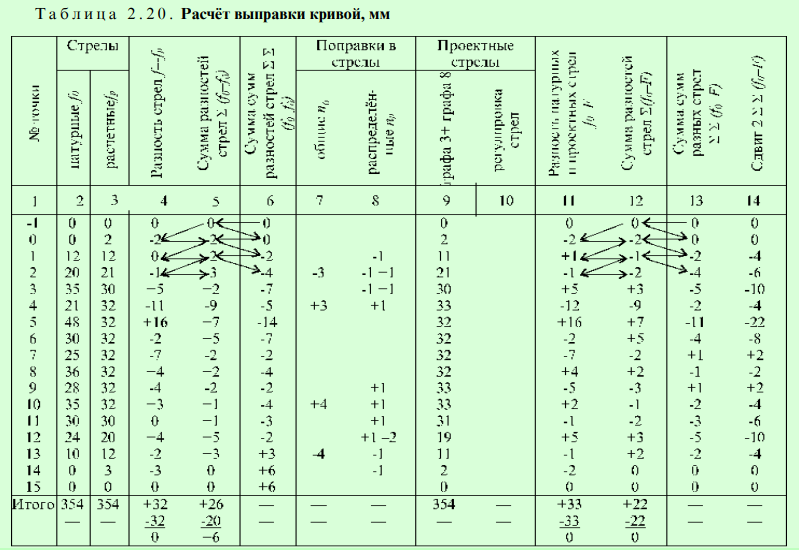
Результаты замеров и “привязки” мест промеров к километрам и пикетам заносят в журнал съёмки кривой (табл. 2.19) и анализи­руют с учётом действующих нормативов.

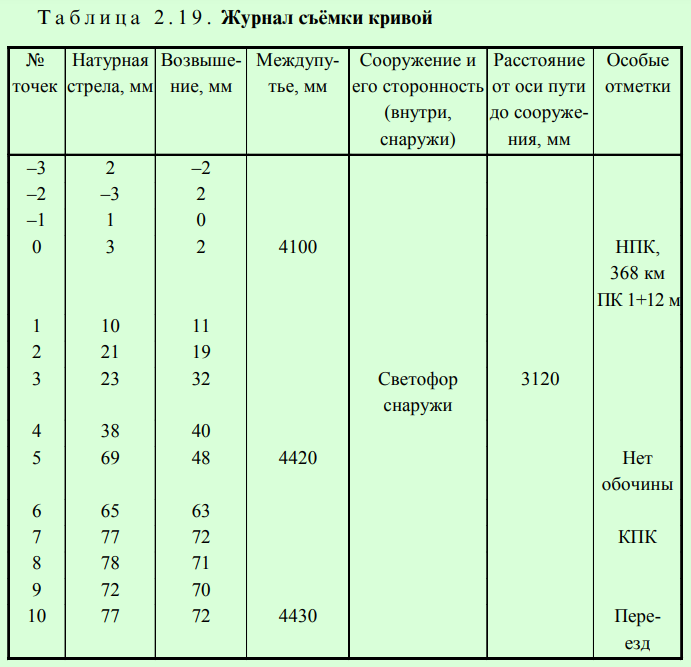
В плане путь должен соответствовать проектному положению. В зависимости от установленной скорости движения поездов положе­ние пути в плане оценивается по разности смежных стрел изгиба рель­совых нитей, измеренных от середины хорды длиной 20 м. При те­кущем содержании пути допуски в разности смежных стрел изгиба в прямых и круговых кривых, а в переходных кривых — отклонения от равномерного роста стрел изгиба не должны превышать: при ско­рости движения 81—140/71—90 км/ч—10 мм; 61—80/61—70 км/ч— 15 мм; 41—60 км/ч—20 мм; 16—40 км/ч—25 мм; 15 км/ч—30 мм.

Все расчёты по выправке кривой базируются на величине на­турных (измеренных) стрел изгиба. Поэтому измеряться они долж­ны как можно точнее.

Материал съёмки кривой направляется в технический отдел ди­станции пути для расчёта на персональном компьютере, или тех­ник рассчитывает её вручную. Результаты расчёта не позднее сле­дующих суток передаются дорожному мастеру для использования при выправке кривой.

Существует немало различных способов расчёта выправки кри­вых, которые основаны преимущественно на одном из двух мето­дов: метод разностей эвольвент, разработанный П.Г. Козийчуком, и метод последовательных приближений, впервые предложенный И.П. Шершавиным.

Эти методы используют основную зависимость проектных стрел от натурных стрел и сдвигов (рис. 2.18).

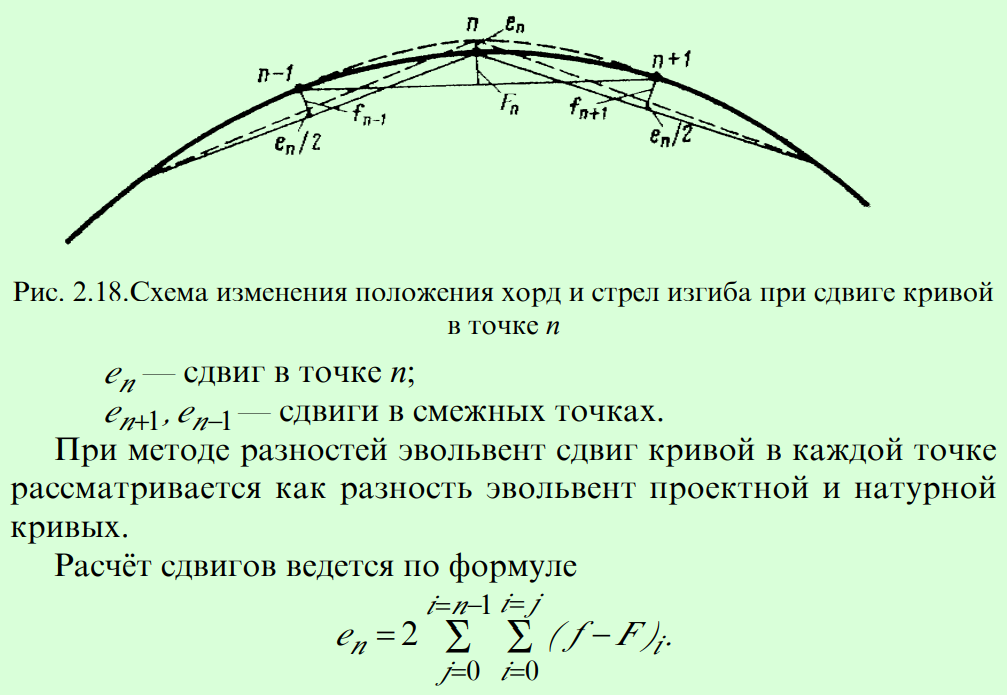
При расчёте кривой методом разностей эвольвент погрешности при определении сдвигов в точках делений кривой увеличиваются по мере их удаления от начала кривой и по мере наращивания ве­личины сдвигов. Однако разности погрешностей в соседних точ­ках не превышают неизбежных погрешностей, допускаемых при измерениях. Поэтому метод разностей эвольвент применяют, ког­да кривая не сильно сбита, т.е. когда сдвиги небольшие и по протя­жению кривой меняются по знаку.

Метод последовательных приближений основан на геометричес­кой зависимости стрелы изгиба в каждой точке кривой от сдвигов в соседних с ней точках. В этом методе сдвиги определяются в ходе постепенного приближения к принятым расчётным стрелам:

При расчёте по методу последовательных приближений вели­чины сдвигов получаются меньшими, чем при расчёте по методу разности эвольвент, и стрелы отличаются от проектных в пределах допусков. Однако многократное применение этого метода может привести к потере проектного положения кривой.

Для постановки кривой в проектное положение следует приме­нять метод разности эвольвент.

На методе последовательных приближений основан и самый простой способ расчёта выправки кривых, использующий зави­симость проектных стрел от натурных стрел и сдвигов, изобра­жённую на рис. 2.19.

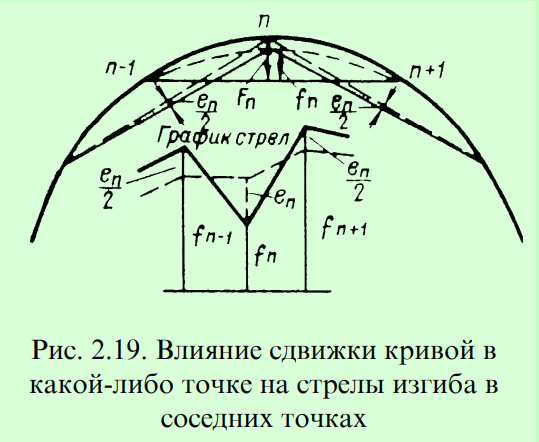
Этот принцип реализован в способе попыток и применён в при­боре конструкции И.Я.Туровского для механизированного расчё­та выправки кривых.

Способ попыток может быть применен и в обычных условиях непосредственно на пути, когда требуется срочно устранить отступ­ления в плане в отдельных точках кривой.

Наибольшее распространение получили графические расчёты выправки кривых, разработанные инженерами А.Т. Крагелем, Г.П. Бредюком, М.Д. Поликарповым, М.А. Макуровым, а также способ последовательного приближения И.Я.Туровского.

Ниже подробно рассматривается способ М.Д. Поликарпова. Исходные данные для расчёта выправки кривой получают при её съёмке. После измерения стрел во всех точках кривой и на приле­гающих участках прямой подсчитывают их сумму. Она характери­зует угол поворота кривой. Поэтому она, как и угол поворота, ве­личина постоянная. Сравнивая сумму измеренных стрел с суммой проектных стрел для данной кривой, можно проверить, насколько точно выполнена съёмка.

Разность между суммами проектных и измеренных стрел, независимо от длины хорды, не должна превышать (в мм):

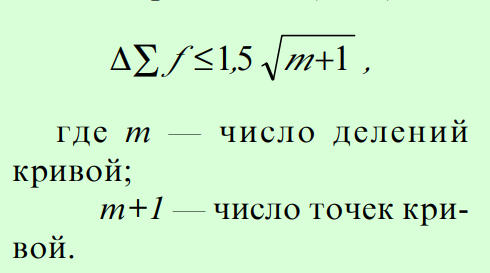
Графоаналитический спо — соб расчёта выправки кривых не дает сразу прямого решения последовательных приближений. Первый этап расчёта заключает­ся в том, что на основании натурных стрел задаются первым вари­антом проектных стрел (расчётные стрелы) и проверяют, удовлет­воряют ли они требованиям, предъявляемым к выправленной кри­вой. Если не удовлетворяют, то проводят второй этап выправки кривой: в первый вариант расчётных стрел вносят коррективы, по­зволяющие прийти к требуемому условию.

В качестве примера рассмотрим расчёт выправки кривой, име­ющей общую длину 140 м. Кривая однорадиусная, с одинаковыми переходными кривыми длиной по 30 м.

Если проектные стрелы неизвестны или не соответствуют фак­тическому положению кривой, первый вариант проектных (расчёт­ных) стрел определяют по натурным данным.

Для этого строят график натурных стрел (рис. 2.20). График стрел вычерчивают, как правило, на миллиметровой бумаге в масштабах: горизонтальный — одно деление кривой в 1 см, вертикальный — 1:1. Под осью графика помещают четыре горизонтальные строки для натурных, расчётных, проектных стрел и для номеров точек делений кривой.

Натурные стрелы записывают в соответствующую графу гра­фика и по ним составляют график натурных стрел. Затем на этом графике строят график расчётных стрел, причём ось этого графика совмещают с осью графика натурных стрел (см. рис. 2.20).

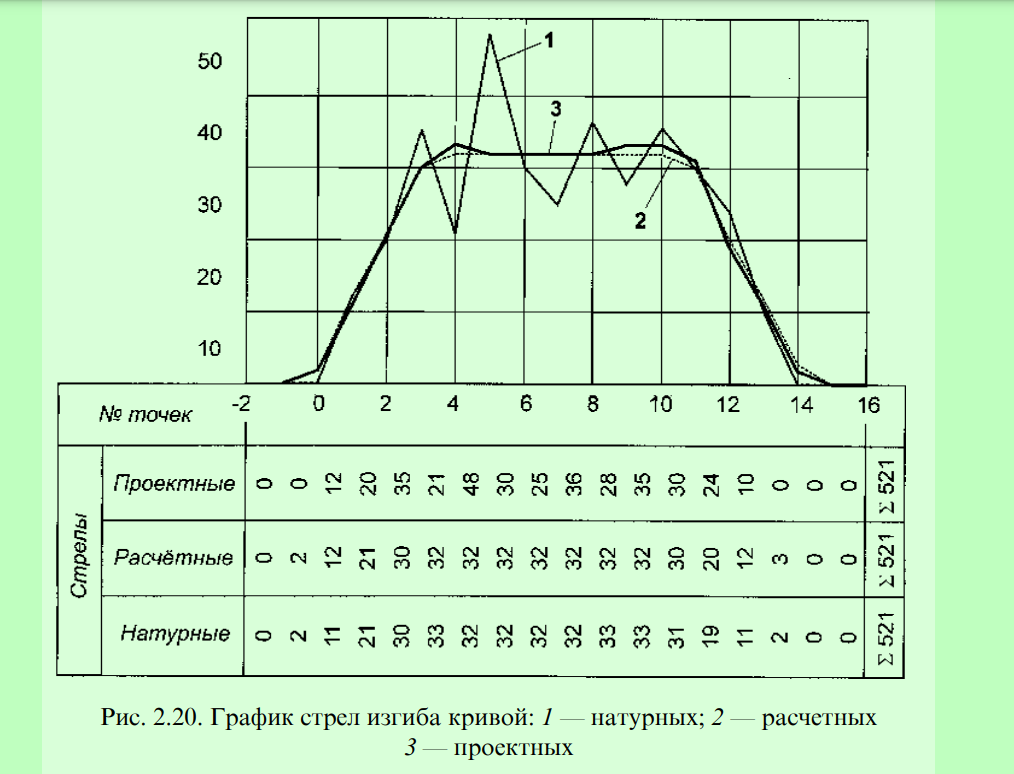
Используя известную длину переходных кривых, ориентировоч­но намечают положение точек НПК и КПК напротив мест предпо­лагаемых вершин углов трапеции проектной линии стрел изгиба. Линию графика расчётных стрел следует наметить так, чтобы она возможно большее число раз пересекала линию натурных стрел. При этом на участке круговой кривой её проводят параллельно оси графика, а на участках переходных кривых — под углом, величина которого зависит от длины переходной кривой и расчётной стре­лы круговой кривой.

Для уточнения положения горизонтальной линии предполагае­мой круговой кривой определяют среднюю расчётную стрелу кру­говой кривой как частное от деления суммы натурных стрел на число точек, входящих в этот участок:

По полученным значениям стрел строят график расчётных стрел и в соответствующую строку графика записывают значения рас­чётных стрел для каждой точки кривой. Подсчитывают сумму рас­чётных и натурных стрел изгиба кривой. Поскольку угол поворота кривой следует сохранить неизменным, должно быть выполнено условие равенства суммы натурных и расчётных стрел изгиба:

В первой строке графы 5 проставляют нуль, во второй строке — число второй строки графы 4, к нему прибавляют число третьей строки графы 5 и т.д. (в таблице это показано стрелками). Контро­лем правильности вычислений является равенство нулю суммы раз­ностей стрел в последней точке кривой (точка 15). Кроме того, должно быть выполнено условие равенства суммы сумм расчётных и натурных стрел:

Для этого во второй строке графы 6 проставляют нуль, к нему прибавляют число второй строки графы 5 и результат записывают в третью строку графы 6, затем к полученной сумме прибавляют число третьей строки графы 5 и результат помещают в четвёртую строку графы 6 и т.д. (в таблице это показано стрелками). Величи­на полусдвига в последней строке графы 6 должна быть равна ито­гу графы 5, иначе графа 6 вычислена неверно.

Контролем правильности подбора первого варианта расчётных стрел является равенство нулю полусдвига в последней точке кри­вой (в последней точке графы 6 полусдвиг получился равным +6). Для того чтобы было выполнено это условие, необходимо откор­ректировать первый вариант расчётных стрел.

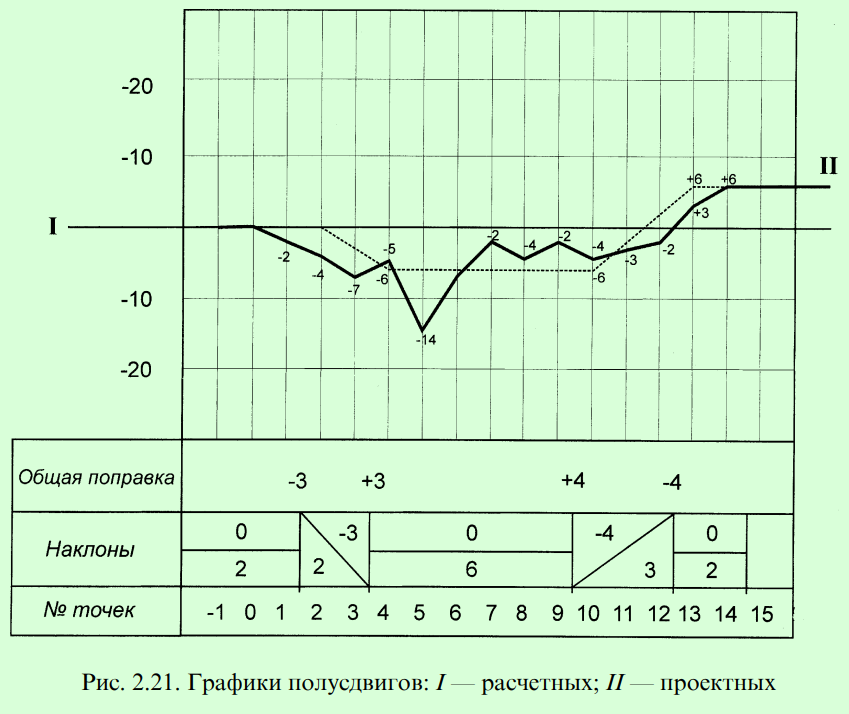
Корректировка расчётных стрел и, следовательно, сдвижек вы­полняется с помощью графика полусдвигов (рис. 2.21). График по­лусдвигов вычерчивают на основании данных графы 6 в масшта­бе: горизонтальный — такой же, как и для графика стрел, верти­кальный выбирают в зависимости от размеров расчётных полусдви­гов в пределах от 1:1 до 1:10. При этом отрицательные полусдвиги откладывают вниз от оси абсцисс, а положительные — вверх.

Этот график в физическом смысле характеризует взаимное по­ложение натурной и расчётной кривых. Если выпрямить расчёт

ную кривую, превратив её в ось абсцисс, и от неё отложить полу­сдвиги, то получим утрированный план натурной кривой. В на­шем случае ось абсцисс 1-1 графика полусдвигов изображает вып­рямленную расчётную кривую, стрелы изгиба которой записаны в графе 3, а кривая графика изображает положение натурной кри­вой. График даёт представление о том, насколько удачно подобра­ны расчётные стрелы. Так, на графике полусдвигов, изображённом на рис. 2.21, видно, что кривая в последней точке расчёта, распо­ложенной на прямой (точка 13), не сопряжена с осью абсцисс и не приняла горизонтального положения. По этому же графику мож­но судить, насколько приемлемы полученные сдвиги по абсолют­ной величине, частоте перемены знака в точках и равенству суммы положительных и отрицательных сдвигов.

Корректируют расчётные стрелы нанесением на график полу­сдвигов линии новой проектной кривой 2. При этом проектная линия должна сопрягаться в начальной и конечной точках с линий полусдвигов 1 для того, чтобы в месте сопряжения кривой с пря­мым участком пути сдвиг был равен нулю, то есть она должна на­чинаться на линии 1-1 и заканчиваться на горизонтальной линии II­II, проходящей через последнюю точку графика. Между началь­ными и конечными точками проектная линия 2 может проходить как угодно (со спусками, площадками и подъемами). В целях обес­печения равенства положительных и отрицательных сдвигов про­ектную линию проводят так, чтобы она как можно чаще пересека­ла линию полусдвигов и чтобы площади, образующиеся между но­вой линией и линией графика полусдвигов, были примерно равны между собой. При наличии ограничений по сдвигам новую линию проводят таким образом, чтобы сдвиги на этом участке не превы­шали необходимых величин или были бы одного знака. Это мож­но определить по графику, зная, что расстояние от проектной ли­нии 2 до линии расчётных полусдвигов 1 равно величине проект­ных полусдвигов. При наличии фиксированной точки, в которой сдвиг должен быть равен нулю, проектная линия должна обязатель­но пройти через эту точку.

Если проектная линия располагается ниже линии расчётных полу­сдвигов, проектный полусдвиг будет со знаком плюс, если выше — минус (плюс — сдвиг наружу кривой, минус — внутрь кривой).

Переломы проектной линии назначают для приближения её к линии расчётных полусдвигов, а следовательно, и получения ми­нимальных сдвигов. Для упрощения расчётов переломы должны совпадать с делениями кривой. Каждый перелом — это поправка в первый вариант расчётных стрел. Крутые переломы лучше распо­лагать ближе к середине круговых и переходных кривых, что по­зволяет более равномерно распределить поправки по точкам. Раз­меры поправок определяют по наклонам проектной линии отно­сительно оси 1-1.

Величину наклона устанавливают делением разности ординат в смежных точках перелома на расстояние между точками, выражен­ное в делениях кривой. Полученное значение должно быть обяза­тельно целым.

Так, величина наклона проектной линии между точками 2 и 4 равна

Знак наклона при подъёме плюс, а при спуске минус. Размеры поправок в расчётные стрелы определяют для каждого перелома проектной линии. Поправка в точке перелома проектной линии равна алгебраической разности значений наклонов последующего и предыдущего участков проектной линии.

Так, общая поправка в точке 13 будет равна: 0 — (+4) = — 4, в точке 10 составит: +4 — (0) = + 4, в точке 4 будет: 0 — (-3) = + 3 и в точке 2 будет: — 3 — (0) = — 3.

Сумма всех поправок должна быть всегда равна нулю, иначе нарушится равенство сумм натурных и проектных стрел.

В рассматриваемом примере: — 4 + 4 + 3 — 3 = 0.

Общие поправки записываются в соответствующую графу гра­фика полусдвигов, а затем в графу 7 табл. 2.20. Общие поправки, как правило, получаются значительных размеров, поэтому их в графу 8 распределяют на ряд точек, если возможно, симметрично в обе стороны от перелома. Необходимо стремиться к тому, чтобы переход от одной величины поправки к другой был без резких скач­ков. Разность в величине скачка должна быть 1—2 мм и не более 3 мм. Симметричное распределение общей поправки не изменяет общего направления проектной линии, а лишь заменяет один кру­той перелом несколькими пологими переломами. В точки, где кри­вая не должна сдвигаться, поправки не вносятся. Графа 9 заполня­ется данными графы 3 с учётом поправок из графы 8. Может ока­заться, что на одну и ту же точку приходится две, а иногда и три поправки, например, в точках 2, 3 и 12 рассматриваемого приме­ра. В этом случае поправка в расчётную стрелу будет равна алгеб­раической сумме распределённых поправок для одной и той же точки.